La brachistochrone

La formulation et la nécessité de l’énoncé de problèmes d’optimisation ne date pas d’hier. Déjà Virgile, dans l’Énéide, raconte comment Didon, à la fondation de Carthage, cherchait le moyen de délimiter la plus grande superficie possible à l’aide d’un périmètre donné figuré par des lanières découpées dans la peau d’un taureau. Dans ce cas, la solution est simple : il s’agit d’un cercle ! Le plus souvent pourtant, ce type de problème lié à une recherche d’extremum (minimum ou maximum) est assez féroce et requiert l’usage de mathématiques avancées (calcul de variations). Au-delà de l’aspect formel, les questions soulevées sont fascinantes et débouchent sur des lois presque philosophiques dans lesquelles s’exprime une nature qui semble guidée par la modération, la plus faible énergie, le moindre effort ou la moindre action.

En juin 1658, le jeune géomètre et mécanicien Christiaan Huygens reçoit d’un auteur anonyme quelques questions relatives à une courbe méconnue : la cycloïde. Appelée jadis la « roulette », il s’agit de la courbe engendrée par l’un des points du bord d’un cercle qui roule sans glisser sur un plan horizontal.

L’anonyme n’est autre que Blaise Pascal qui, d’ailleurs, lance un défi aux mathématiciens de son temps, assorti d’un prix de 60 pistoles, sur ce même sujet d’étude : la roulette. Huygens participe à ce concours et est amené à utiliser les propriétés de la cycloïde pour la réalisation d’horloges capables de répondre au problème de la détermination de la longitude. En effet, pour mesurer la longitude d’un lieu, il suffit de connaître le décalage horaire entre ce même lieu et le point de départ ; malheureusement, les horloges de l’époque supportaient mal l’instabilité du pont des bateaux.

Pour fabriquer une horloge fiable, on pourrait d’abord penser au pendule simple, mais celui-ci n’a pas une période constante ; elle dépend de l’amplitude (à moins de fixer l’amplitude pour que le battement soit régulier mais, même dans ce cas, les dilatations dues aux variations de température feront varier la période). C’est là qu’Huygens retrouve la cycloïde, dont les propriétés mécaniques sont très intéressantes.

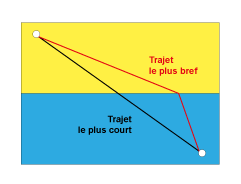
Laissons tomber 2 billes d’un même point. L’une suit une pente rectiligne et l’autre une piste en forme de cycloïde.

Si nous comparons les durées de chute des deux billes, le chemin qui s’avère « le plus vite » (le trajet le plus bref, en vieux français) est celui qui emprunte un arc de cycloïde : c’est la brachistochrone. L’arc de cycloïde s’avère d’ailleurs le chemin le plus court parmi tous les autres reliant les mêmes points de départ et d’arrivée.

Mieux encore, l’arc de cycloïde est même une tautochrone : le temps que mettent deux billes pour atteindre le point d’arrivée est indépendant de l’endroit à partir duquel on les lâche !
C’est cette dernière caractéristique qu’Huygens utilisa pour fabriquer un pendule parfaitement isochrone, le pendule cycloïdal (« horloge oscillante » en 1673).

Un autre problème de minimisation fut posé par Jean Bernoulli à la fin du XVII^e siècle : considérez les deux points placés dans les coins opposés de la surface ci-contre et admettons qu’il faille aller de l’un à l’autre dans le temps le plus court possible. Sachant que dans la partie supérieure (la plage, en jaune), la vitesse est 4 m/s et que, dans la partie inférieure (la mer), la vitesse plus faible est 3 m/s, quel sera le trajet le plus bref ? De façon un peu surprenante, la solution (noir, en trait plein) est le chemin que suivrait la lumière passant d’un point à l’autre en se réfractant en changeant de milieu de propagation (car l'indice de réfraction de l'eau est 4/3). Le problème avait déjà été résolu quelque vingt ans plus tôt, en optique, par Pierre de Fermat, et érigé en principe qui peut remplacer les lois fondamentales de l’optique : la lumière emprunte toujours le chemin le plus bref d’un point à un autre.

Ce principe, qui affirme élégamment l’existence d’une règle d’économie de la nature, fera école et sera le sujet d’un débat animé au XVIII^e siècle quand le principe de moindre action de Maupertuis divisera la pensée scientifique. D’un côté, ceux pour qui l’existence des lois basées sur les maxima et minima sont la traduction de la cause parfaite qu’est Dieu et, de l’autre, ceux qui répugnent à mêler arguments philosophiques et science et qui ne voient dans ces principes que la représentation mathématique de l’efficacité des lois physiques.

Repensons à la brachistochrone : dans le champ de pesanteur où la vitesse d’un objet augmente régulièrement au cours de la chute, la courbe la plus rapide est la cycloïde. Si nous parvenons à créer un milieu transparent dans lequel la vitesse de la lumière augmente progressivement de haut en bas, nous pourrons la conduire à adopter un trajet – un chemin optique de durée minimale – de type cycloïdal (Jean Bernoulli 1696). Ce genre de trajectoire lumineuse est obtenu lors de la formation des mirages.